Beskonačna konačnost 52. broja

Beskonačna konačnost 52. broja

Black holes result from God dividing the universe by zero..(n/a)

8 0 6 5 8 1 7 5 1 7 0 9 4 3 8 7 8 5 7 1 6 6 0 6 3 6 8 5 6 4 0 3 7 6 6 9 7 5 2 8 9 5 0 5 4 4 0 8 8 3 2 7 7 8 2 4 0 0 0 0 0 0 0 0 0 0 0 0

Mešanjem špila karata koliko je permutacija moguće dobiti? Odnosno, koliko različitih kombinacija? Matematički gledano, skoro pa da ne postoji način da nakon mešanja izvučete kombinaciju koju je iko ikada pre vas izvukao, te je tako raspored karata u vašim rukama apsolutno jedinstven još od momenta nastanka karata kao takvih. Čak i mnogo više od toga. To je jedinstvena kombinacija u čitavom univerzumu, još od njegovog postanka pre nekih 14 milijardi godina i upravo tu, u toj simbolici, leži nepojmljiva snaga matematičkog faktorijela (n!), odnosno faktorijela broja pedeset i dva.

Radi se o redu broja tolike tolike veličine i simbolike da je o tome, ovako usput, krajnje nelagodno diskutovati, a posebno plastično analizirati što planiramo u nastavku teksta.

Ali valjda će nam oprostiti bogovi beskonačnosti na onome što sledi…

Ipak smo samo ljudi.

52!

So, if you are ever feeling boring or predictable, just remember that you are made out of octillions of quantum probabilities. Dice that don’t tumble in any analysable way we could ever predict, they are the most random thing…

God may play dice with the universe, but they are the best dice in the universe.

Dakle faktorijel predstavlja matematičku funkciju kojom se računa proizvod prirodnih brojeva od 1 pa do nekog određenog prirodnog broja n. Koristi se ponajviše u statistici, kao i u zakonima verovatnoće i kombinatorici, a karakterističnu notaciju – n! – uveo je francuski matematičar Kristijan Kramp (Christian Kramp) sada već davne 1808. godine.

Na prvi pogled u ovom eksperimentu sve započinje više nego bezazleno: 52 tanko isečena komada plastike, šarenolikog dizajna, gde kao i kod svake mantričke ilustracije najveća kompleksnost započinje iz apsolutne jednostavnosti, jer broj kombinacija sa kojim ćemo se upravo suočiti skoro pa da možemo svrstati u red beskraja, te da realno kontempliramo o nečemu tako apstraktnom.

Sâm princip faktorijela je u sledećem: ukoliko u ruci držimo tri karte, ukupan broj njihovih permutacija iznosi 6, odnosno:

3! = 3 x 2 x 1

Ukoliko, pak, raspolažemo s 5 karata, rezultat je:

5!= 5 x 4 x 3 x 2 x 1 = 120 permutacija.

Dakle 120 permutacija ili sto dvadeset jedinstvenih načina da ih rasporedimo.

Ali, kada je reč o celom špilu karata, ukupni broj permutacija je sledeći:

52! = 52 x 51 x 50 x 49… x 1 = 8.0658175e+67

80 658 175 170 943 878 571 660 636 856 403 766
975 289 505 440 883 277 824 000 000 000 000

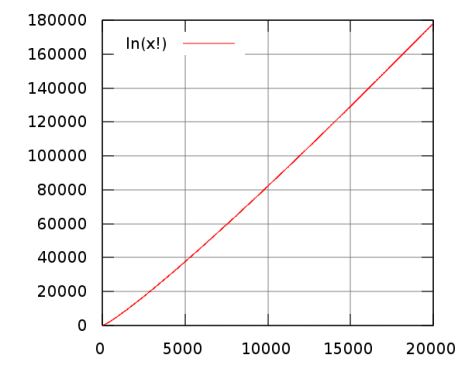
Realna veličina ovog broja nadmašuje i najluđe kosmičke veličine koje čovečiji um uopšte može da prihvati i pojmi. A ukoliko bi, makar teoretski, želeli da prođemo kroz svaku permutaciju u špilu, koliko nam je mešanja za to potrebno? Koliko vremena? Ako bi nam, primera radi, jedna sekunda bila dovoljna za jedno mešanje karata, koliko bi nam sekundi ukupno za to trebalo trebalo? Nakon kog vremena bi izvukli prvu ponovljenu kombinaciju rasporeda?

Mora se proći kroz 52! sekunde mešanja ne bi li se tako nešto i dogodilo, te u narednom detaljnom misaonom eksperimentu ova problematika dobiće svoju vrlu slikovitu predstavu, odnosno biće skrenuta pažnja na to koliko u stvari nismo spremni da se mentalno uhvatimo u koštac s brojevima ovog ranga. Ili čak i većim (!?). Počećemo tako što ćemo zamisliti da se sa našim špilom karata nalazimo na nekoj prozvoljnoj tački na ekvatoru naše planete (jer je na liniji ekvatora planeta Zemlja najšira, što je za naš opit od izuzetnog značaja), odakle planiramo da započnemo s eskperimentom istraživanja realne veličine faktorijela broja 52.

Dakle, odrađivaćemo po jedno mešanje špila svake sekunde… Zatim drugo mešanje. Treće mešanje. Četvrto… Tako radimo narednih milijardu (brojevima: 1,000,000,000) godina. Stojeći na početnoj tački na ekvatoru i mešajući, tek nakon tih milijardu godina činimo prvi korak napred, s mesta na kojem smo počeli s eksperimentom (pre milijardu godina). Dakle, špil ponovo mešamo godinama, dekadama, vekovima, milenijumima, stotinama milenijuma, hiljadama… i nakon milijardu godina činimo taj jedan običan, jedva metar dugačak, korak. Nakon toga se ponovo zaustavljamo i nepomično nastavljamo s mešanjem. Prolazi i drugih milijardu godina nakon kojih pravimo i drugi korak…

I dalje nastavljamo s mešanjem. Posle pet milijardi godina, što je malo više od ukupnog vremenskog intervala koliko i postoji ova naša planeta Zemlja, načinili smo ukupno pet koraka od mesta gde smo sve i započeli. Svega par metara za neverovatnih 5 milijardi godina duž puta dugog ukupno 40,075 kilometara. Naš zadatak se potom nastavlja sve dok ne obiđemo planetu duž ekvatorijalne linije, krećući se istim tempom na svakih milijardu godina.

Tom brzinom koračamo duž čitavih kontinenata i okeanskih prostranstava… korak po korak.

Čisto poređenja radi, obilaženje jednog kruga oko naše planete, ekvatorijalnom rutom, brzinom od jednog metra u milijardi godina trajalo bi oko 1.264e24 sekundi, ukoliko uzmemo u obzir da odrasla osoba, u proseku, jednim korakom pređe rastojanje od jednog metra. S druge strane, vrednost od 1.264e24 sekundi gotovo tri puta nadmašuje trenutnu starost našeg celokupnog kosmosa, procenjenog na oko 14 milijardi godina.

Sledeći bitan momenat dešava se kada se nakon enormno mnogo vremena neprekidnog koračanja i mešanja karata duž ekvatora, korak po korak na svakih milijardu godina, ponovo nađemo na istoj tački sa koje smo i pošli u našu apstraktnu avanturu. Nakon što smo kompletirali prvi krug oko planete, sada pipetom iz Tihog okeana uzimamo jednu kap vode. Jednu jedinu kap! I nakon što smo je izdvojili iz vodene zapremine najvećeg okeana na planeti, vraćamo se našem mešanju i novom krugu koračanja duž linije ekvatora. Započinjemo drugi krug, istim tempom – korak na svakih milijardu godina… Sve dok se opet ne nađemo na mestu s kojeg smo krenuli, kada uzimamo i drugu kap vode iz Pacifika.

Već u ovom momentu, nakon dva kruga, radi se o nečemu što traje čitavu večnost, čak i u vremenskim okvirima našeg kosmosa, a za svo to vreme mi smo izdvojili tek dve kapi vode iz najvećeg okeana. I i dalje nastavljamo da se krećemo oko planete, istom brzinom, korakom na svakih milijardu godina, iznova, iznova i iznova, sve dok se opet ne nađemo na našoj početnoj tački ali u trenutku kada našom pipetom ne odstranimo i poslednju kap vode iz Tihog okeana. Sada kada smo, kap-po-kap, ispraznili ceo Pacifik dobijamo prazan list papira, koji polažemo na zemlju. Taj papir je sve što dobijamo nakon svega što smo prošli; nakon beskrajnog koračanja na svakih milijardu godina; nakon uzimanja po jedne kapi vode iz Tihog okeana svaki put kada bi prepešačili čitavu planetu; pa sve do pražnjenja te enormne zapremine vode.

Sada, kada je čitav okean ispražnjen, ceo proces ponavljamo ispočetka. Pacifik je ponovo napunjen vodom i mi iznova krećemo u koračanje na svakih milijardu godina i uzimanja kapi vode iz okeana, nakon obilaženja planete…

Nakon još jedne, malo je reći večnosti, Tihi okean ponovo biva ispražnjen i mi dobijamo još jedan, drugi, list papira. Sada ih imamo dva i to je znak da ponovo krećemo u novu turu pešačenja. Sve ponavljamo. Jedan po jedan list dodajemo, sve dok ta gomila papira ne bude dužine rastojanja od Zemlje do Sunca, odnosno jedne astronomske jedinice (astronomical unit, AU) koja je i definisana tim rastojanjem i iznosi nekih 149,597,870 kilometara. Dakle, gomila papira visoka impozantnih 150 miliona kilometara, a sve naslagano postepenim dodavanjem jednog po jednog lista hartije za svo pređašnje obilaženje planete brzinom od jednog koraka na svakih milijardu godina, te pražnjenja okeana kap-po-kap. I da, da ne zaboravimo, svo ovo vreme traje mešanje naših karata, bez prekida. Da li tu završavamo našu potragu za prvim ponovljenim nizom od 52 karte, koje, uzgreg, već sada večno traje?

Ne. Potrebno je još jedna gomila tog papira dužine jedne astronomske jedinice, te nastavljamo s dodavanjem po jednog lista kako praznimo okean. Za konačan kraj ove torture dostojne najstrašnijeg kosmičkog horora kome nema kraja potrebno nam je ukupno čak 3.000 tih gomila, svaka dužine astronomske jedinice. Pakleno gomilanje koje moramo da ponovimo 3.000 puta i tek nakon toga završavamo s mešanjem karata i tada smo u potpunosti dosegli punu vrednost faktorijela broja 52. Odnosno svih mogućih permutacija.

To je ta sirova moć broja koji se krije iza 52!, skriveni potencijal koji leži u svakom špilu karata. Špilu ušuškanom u svojoj kutiji u fioci, a u čijoj se matematičkoj senci vešto skriva punokrvni demon večnosti, spreman da nas goni u pakao beskrajnih brojeva i nesagledivih prostranstava vremena, kojem nema kraja. I koji definitivno ne razumemo…

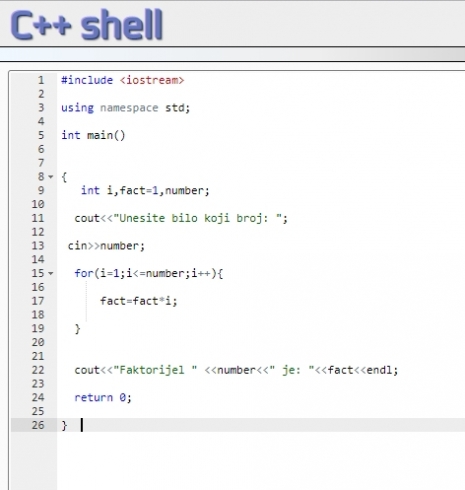
S druge strane, paradoksalno, vrednost 52! možemo ručno ispisati za nekih tridesetak sekundi, nepun minut i kao takav daleko je manji od mnogih drugih zaista velikih brojeva. 52! sadrži svega 67 cifara, što je u poređenju s brojem kao što je npr. gugol (googol, 10¹⁰⁰) daleko manje, jer je gugol reda veličine jedinice sa sto pratećih nula… A što je opet ništa u poređenju s gugolpleksom. Gugolpleks je 1 sa 10 na stotom nula (googolplex, 10^10*100), te ako bi taj broj probali makar i ručno da ispišemo, u samom startu bi naišli na nepremostiv fizički problem – jer broj nula gugolpleksa daleko premašuje broj atoma od kojih je satkan nama dostupan i merljiv svemir.

Nastavimo li u ovom ritmu i maniru s igranjem brojevima, postoji realna mogućnost da završimo upadajući u paradoksalnu crvotočinu problematike, analize i pokušaja razumevanja Gremovog broja (Graham’s number), gde onda postoji i velika izvesnost gubitka razuma spram Broja koji bi stavili pred nas…

Albert Ajnštajn je jednom prilikom rekao da se bog ne kocka.

I u pravu je bio. Ne kocka se.

On je krupije za zelenim stolom Postanja.

Zato ćemo sada, i ovde, stati.