Njutnova mehanika nam već nekoliko stoleća daje moćan alat da prilicno precizno predvidimo, ne samo pomračenja, Sunca i Meseca već i mnoge druge astronomske događaje u širokim vremenskim intervalima. Tako možemo da izračunamo da li se i kada, recimo 2000. godine pre nove ere moglo videti pomračenje Meseca iz južne Engleske. Da li je moguće da su i tadašnji lovci britanskog ostrva mogli da znaju za to pomračenje pre no što je ono počelo?

Arheoastronomske metode i arheološko-astronomske prepirke

Džerald Hokins (Gerald Hawkins), profesor astronomije sa Bostonskog univerziteta, svojedobno je uzburakao naučnu javnost tvrdeći da je odgovor na ovo pitanje potvrdan. Šezdesetih godina minulog stoleća on je objavio članak u casopisu Nature, a potom i knjigu, gde saopštava da je otkrio na koji je način Stounhendž (Stonehenge), poznata monumentalna kamena građevina u južnoj Engleskoj, služila u praistoriji, ne samo kao svojevrsna astronomska opservatorija, već i kao računar za predviđanje pomračenja. Kako dotična Hokinsova knjiga (Stonehenge Decoded – rešena tajna Stounhendža) sadrži i problematične postavke, njegove su tvrdnje bile oštro osporavane u nekim akademskim krugovima, a naročito među arheolozima.

Međutim, prvi naučnik koji istražuje Stounhendž sa astronomskog stanovišta bio je Sir Norman Lokjer (Lockyer, 1836-1920), poznati naučnik toga doba. Lokjer je, između ostalog, 1859. godine osnovao danas čuveni Nature, a potom izvesno vreme radio kao njegov urednik. Astronomi ga najviše pamte po otkriću helijuma na Suncu. Arheolozima je, ipak, najviše ostao poznat upravo po svojoj astronomskoj interpretaciji funkcije pojedinih lokaliteta.

Tokom putovanja po Mediteranu i Egiptu Lokjer konstatuje da su neki hramovi orijentisani prema izlasku Sunca. Između ostalog utvrđuje da je glavna osa Amonovog hrama u Karnaku usmerena ka tački gde izlazi Sunce za vreme letnjeg solsticijuma. Potom analizira i Stounhendž, gde konstatuje da su ovde, osim solsticijuma, markirane i ravnodnevnice. Zajedno sa F. Penrouzom (Penrose) sprovodi merenja istaknutih pravaca na spomeniku i na onovu njih ga datuje na 1860. godinu pre nove ere. Na koji način? Poznato je da Sunce izlazi najsevernije na horizontu na dan letnjeg solsticijuma. Zbog precesije Zemljine ose rotacije, ova tačka se lagano pomera, usled čega se za četiri milenijuma, za geografsku širinu Stounhendža, pomerila nešto manje od jednog stepena. Dakle, ovo pomeranje je veoma malo i iznosi 0.02 stepena za jedno stoleće. Pošto je glavna osa usmerena ka severoistoku, tačnije ka tacki blizu koje sada izlazi Sunce za vreme letnjeg solsticijuma, Lokjer teodolitom meri njen azimut za koji, nakon korekcija, dobija srednju vrednost od 49.5717 stepeni. Na osnovu razlike u azimutima izmedu sadašnjeg izlaska Sunca u vreme letnje dugodnevnice i izmerene vrednosti, dolazi do navedene vrednosti koju, zbog mogucih grešaka aproksimira na vremenski period od 1900. i 1500. godine pre nove ere, smatrajuci da je Stounhendž izgrađen u tom periodu. Iako je Lokjerov metod sa astronomskog stajališta potpuno korektan, arheolozi su se prema njemu postavljali veoma kriticki. Glavna njihova zamerka bila je ta što tačke kojima je definisan mereni pravac ne moraju biti objekti koji su izgrađeni u istom periodu, što su kasnija datovanja i potvrdila. U svakom slučaju, zbog ovih svojih radova mnogi današnji istraživaci Lokjera smatraju ocem arheoastronomije.

No, vratimo se Hokinsu. Za razliku od Lokjera koji analizira nekoliko unapred odabranih, konstrukcijom Stounhedža nametnutih pravaca, on koristi o-ruk sistem. Naime, razmatra praktično sve pravce određene parovima kamenova na spomeniku, a onda, uz pomoć računara, traži među njima one koji imaju astronomski kontekst. Konkretno, on traži pravce koji se odnose se na tačke izlazaka i zalazaka Sunca, Meseca, planeta i nekih sjajnijih zvezda u periodu od 2001. do 1000. godine pre nove ere. Hokins nije našao nikakve pravce koji bi ukazivali na izlaske ili zalaske zvezda i planeta. Medutim, konstatovao je 10 pravaca koji su, sa greškom ne većom od jednog stepena, ukazivali na bitne tačke vezane za istaknute položaje Sunca na horizontu tokom godine. Za Mesec je našao 14 takvih pravaca (neki od tih pravaca oznaceni su na slici).

Krajem šezdesetih i početkom sedamdesetih, arheoastronomska struja dobija pojačanje u radovima profesora Aleksandra Toma (Alexander Thom, 1894-1985). Tom od tridesetih godina sistematski i detaljno geodetski meri arheološke lokalitete u Britaniji. Istražio je ih je oko tri stotine. Posebno se bavi geometrijskim oblicima i geometrijskim odnosima kod neolitskih gradevina. Statističkom analizom samerljivosti najfrekventnijih izmerenih dužina, došao je do zaključka da su tadašnji graditelji imali jedinicu za merenje dužine (megalitski jard, koji iznosi 83 cm)! U istraživanjima mu pomažu sin Arčibald, a i ostali članovi porodice, kada uspeva da ih ubedi. Istraživao je i kamene kolonade u Karnaku (Bretanja, Francuska) i Brodgarov prsten na Orknijskim ostrvima. Do ovog vremena Tom se nije eksplicitno bavio Stounhendžom, smatrajući da svoju pažnju treba da posveti ostalim sličnim, bezrazložno zapostavljenim spomenicima. Sa sebi svojstvenom sistematičnoću on je ponovo izvršio topografska snimanja Stounhendža i ispostavilo se da centralna konstrukcija nije u obliku grube potkovice, već je deo potpuno pravilne elipse. Takode je utvrdio da se na horizontu iz Stounhendža vide i udaljeni orijentiri, ciji položaj omogucava veoma precizna merenja položaja Sunca i Meseca. Atkinson, koji je ranije bio žestok kriticar Hokinsovih spekulacija, sasvim je drugacije reagovao na Tomove argumente. Poneo se kao pravi engleski džentlmen.Upravo na tim nalazima, Hokins u osnovi temelji svoju priču o ‘neolitskom računaru’. Arheolog Ričard Atkinson, jedan od tada vodećih autoriteta za Stounhendž na Hokinsovu ‘Rešenu tajnu Stounhendža’ odgovara ‘Mesečinom iznad Stounhendža’ (Moonshine on Stonehenge). U ovom kritičkom članku koga objavljuje časopis Antiquity, Atkinson proverava kolika je verovatnoća da konstatovani pravci nisu slučajni. Za razliku od Hokinsa, dobija da je rizik takve pretpostavke čak 50%. Hokins se, pak, usmerava na sličan problem u Peruu, lokalitet Naska (Nazca), poznat po neobičnim ogromnim geometrijskim figurama. Devedesetih godina, on se uveliko bavi tajanstvenim geometrijskim formacijama, ali u Engleskoj (crop-circle patterns).

Koliko je polemika oko arheoastronomije, pokrenuta Hokinsovim delima, uzburkala duhove šesdesetih i sedamdesetih godina, ilustruje i činjenica da se u nju uključio i Fred Hojl (Hoyle), poznati engleski astrofizicar, koji nudi svoj model za arheoastronomsko funkcionisanje Stounhendža. Klajv Ragls (Clive Ruggles) sa univerziteta u Lesteru, inače jedan od vodećih arheoastronoma danas u svetu, sigurno ne bez razloga u svojoj knjizi Astronomy in Prehistoric Britain and Ireland, period između 60. i 80. godine minulog veka uzima kao prvu fazu u intenzivnom razvoju arheoastronomije.

Stounhendž kao Altamira

Verovatno zbog toga što je često bio predmet istraživanja i velikih polemika, Stounhendž je postao opšte prepoznatljiv simbol za bavljenje čoveka naukom (naravno, u širem i manje striktnom značenju te reči) u praistoriji, baš kao što su pećine Lasko i Altamira postale simbol za umetnost ljudi Ledenog doba. Međutim, dok ove pećinske slike, stare 25 milenijuma, izazivaju divljenje, Stounhendž i njemu slični spomenici, stari samo oko 5 hiljada godina, najpre – postavljaju pitanja. Naše znanje o njima suviše je površno da bismo pouzdano znali za šta su ove konstrukcije korišcene i kako su funkcionisale. U svakom slučaju, Stounhendž je praistorijski spomenik čije je proučavanje najviše doprinelo utemeljenju proučavanja drevne astronomije.

Stounhendž je, slično drugim takvim građevinama na Britanskim ostrvima, građen u nekoliko faza, pri čemu su prva i poslednja međusobno vremenski udaljene preko hiljadu godina. Više od polovine tog vremena proteklo je od početka gradnje (prve faze) do podizanja velikih megalita koji su danas glavna asocijacija na ovaj spomenik. U razvoju Stounhendža mogu se izdvojiti tri osnovna perioda, ona koje je definisao i razlučio sam Atkinson.

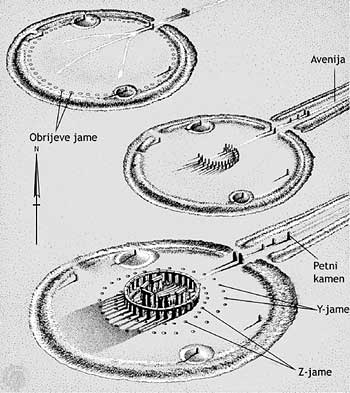
U drugoj fazi, koja se povezuje sa keramičkim nalazima Kulture pehara (Beaker), osim pomenute Avenije, podignut je dvostruki prsten sa 80 stena od pemrokširskog plavičastog kamena. Ovaj kamen potiče sa planina jugozapadnog Velsa, koje su udaljene preko 300 kilometara. Otvor dvostruke kamene kružnice okrenut je u pravcu avenije, tj. ka tački izlaska Sunca za vreme letnjeg solsticijuma. Izgleda da ovaj rani kameni spomenik od delimično obradenih i oklesanih stena nikada nije bio završen.Prvu fazu, datovanu na oko 3000. godine pre nove ere, predstavlja kružni nasip (hendž), 98 metara u prečniku, sa plitkim rovom sa spoljašnje strane. Iz njega je verovatno i iskopavan materijal za gradnju nasipa. Na osnovu širine i dubine rova, procenjuje se da je nasip, kada je izgrađen, bio visok oko 2 metra. Rov je otvoren sa severoistočne strane, odakle počinje tzv. Avenija, prilaz oivičen sa dva paralelna zemljana nasipa. Ona je izgradena kasnije i uglavnom je svrstavaju u drugu fazu. Avenija se u pravoj liniji pruža skoro 300 metara, a potom se se deli na dve grane, od kojih jedna savija ka severu, a druga ka istoku prema reci Ejvon. U okviru zemljanog nasipa, pored njegovog ruba nalazi se prsten od 56 velikih rupa, tzv. Obrijevih jama, nazvanih tako u cast Džona Obrija (Aubrey), koji ih je opisao još u XVII veku. U ovim jamama pronađene su koštane igle i kremirane ljudske kosti, tipično za neolitske kulture sa područja Veseksa. Verovatno da su u njima bili usađeni drveni stubovi, a nakon toga da su služile za skladištenje ostataka ceremonijalnih svetkovina. Prvoj fazi verovatno pripada i jedan usamljeni kamen – tzv. Petna stena (Heelstone), usađena u mali rov unutar Avenije. Takode, tu pripadaju i četiri usamljena kamena uz unutrašnju stranu kružnog nasipa, od kojih su danas samo dva sacuvana (slika iznad).

Najmonumentalniji deo Stounhendža izgrađen je trećoj fazi. Početak ove faze datuje se na 2000. godinu pre nove ere. U njoj je podignut kružni deo od ogromnih sarsenskih stena povezanih poprečnim gredama, po kojima je Stounhendž i danas prepoznatljiv. Unutar prstena potkovičasta forma od trilitona (po dva uspravna kamena sa poprečnom gredom), za koju je Aleksander Tom utvrdio da je deo elipsastog prstena. Sarsenske stene (u pitanju je tercijarni pešcar) dopremljene su sa daljine od 30 kilometara. Monoliti su visoki po 9 metara i teški pet tona. Nakon stotinak godina, od obrađenog kamena iz druge faze, unutar potkovice (zapravo elipse) podignut je ovalni prsten, a oko sarsenskog prstena su iskopane dve kružnice sa po trideset rupa u svakoj, verovatno u nameri da se u njih smeste preostale stene od plavičastog kamena preostale iz faze II.

Ako je ovakva konstrukcija i služila za predviđanje pomračenja, teško je zamisliti da joj je to bila jedina namena. Međutim, priča o funkciji Stounhedža je daleko od namere ovog članka. U daljem tekstu pokušaćemo da, pod pretpostavkom da je ovaj praistorijski spomenik imao i takvu funkciju, predstavimo neke modele koji možda objašnjavaju kako je ona mogla biti ostvarena. Pošto su, gledano iz jednog mesta, pomračenja Meseca znatno frekventnija od Sunčevih, razmatraćemo samo njih.

Ciklusi Mesečevih pomračenja

Pomračenja Meseca su pojave kada se Mesec nalazi u Zemljinoj senci. Zbog toga što Zemlja ima atmosferu koja različito prelama pojedine delove spektra Sunčeve svetlosti, prilikom ovih pomračenja Mesec dobija zanimljivu crvenu boju, a pri intenzivnijim pomračenjima, čini se da Mesec nestaje.

Ova pomračenja se dešavaju onda kada se Mesec i Sunce nalaze na suprotnim stranama u odnosu na Zemlju, dakle, samo onda kada je pun Mesec. Stoga je osnovna vremenska mera za pojavljivanje pomračenja tzv. sinodički mesec, tj. period izmedu dva uzastopna istovetna položaja Meseca u odnosu na Sunce, recimo između dva uzastopna puna (ili mlada) Meseca. Međutim, do pomračenja ne dolazi pri svakom punom Mesecu, pošto se ravni Meseceve putanje oko Zemlje i Zemljine oko Sunca ne poklapaju, već zaklapaju ugao nešto veći od 5 stepeni. Linija po kojoj se ove dve ravni seku naziva se linija čvorova i sadrži dve tačke (čvorove) u kojima Mesec na svom putu oko Zemlje seče ravan ekliptike, tj. ravan Zemljine putanje oko Sunca. Kada se Mesec nađe u jednom od čvorova, tada se Sunce, Zemlja i Mesec nalaze u istoj ravni.

Dakle, pomračenje Meseca se događa samo onda kada se PUN Mesec nađe u blizini jednog od čvorova (Sunce je onda u blizini drugog čvora). Tada se Sunce, Zemlja i Mesec nalaze, ne samo u istoj ravni, već leže i na istoj pravoj. Zbog dimenzija Zemljine senke koja je oko dva puta šira od Meseca, ovaj uslov je donekle ublažen. Naime, do pomračenja može doći kada za vreme punog Meseca Sunce nije udaljeno od čvorova više od 17 stepeni. Pošto se Sunce na ekliptici pomeri približno jedan stepen za jedan dan, to znači da tokom godine u proseku postoje dva kritična perioda od po tridesetak dana kada može doći do pomračenja. Kada je u tim periodima pun Mesec, jedino tada dolazi do pomračenja Meseca.

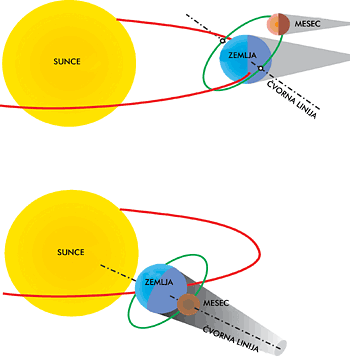
Zemljani radovi za instaliranje računara. Zbog precesije Mesečeve putanje, linija čvorova nije nepokretna, već se kreće po ekliptici, pri čemu napravi pun krug za 18.6 godina. Vreme za koje se Mesec ponovo vrati u isti čvor, tzv. drakonistički mesec, iznosi 27.212220 dana i nešto je kraće od vremena koje protekne između dva uzastopna puna Meseca, tj. sinodičkog meseca koji iznosi 29.5330589 dana. Rezonancijom ova dva perioda nastaje saros, vremenski interval nakon kojeg Mesec i Sunce ponavljaju isti uzajamni položaj u odnosu na Zemlju, pa se i pomračenja ponavljaju istim redosledom kao u prethodnom ciklusu. Naime, jedan saros sadrži 223 sinodička meseca, odnosno 6585.321124 dana. To, s druge strane, iznosi 241.998, tj. približno CELA 242 drakonistička meseca. Kako je u pitanju ceo broj drakonističkih meseci, Mesec zauzima isti položaj i u odnosu na čvorove. Od početka do kraja sarosa protekne 18 godina i 11 1/3 dana, odnosno 10 1/3 dana, ukoliko u period ulazi pet prestupnih godina. Zbog 1/3 dana ‘viška’ u sarosu, pomračenja se u sledećem ciklusu dešavaju oko 120 stepeni zapadnije, time i 8 sati kasnije u odnosu na odgovarajuće pomračenje iz prethodnog ciklusa. Nakon tri sarosa, tj. oko 54 godine i jednog meseca, položaji se skoro u potpunosti ponavljaju. Na primer, ako je 9. januara uveče 2001. godine bilo pomračenje Meseca, ono će se desiti i 2019. godine 23. januara ujutro. Pomračenje 31. januara 2037. godine se neće videti, jer će pasti za vreme obdanice, kada je pun Mesec ispod horizonta. Pomračenje 11. februara 2055. godine će većim delom biti u prvoj polovini noći, dakle u približno isto vreme kada je bilo i 9. januara 2001.

Kako bez znanja nebeske mehanike ‘provaliti’ ovaj sistem? Kao što je rečeno, da bi došlo do pomračenja Meseca, potrebno je prvo, da je pun Mesec i, drugo, da je Sunce u blizini jednog od čvorova Mesečeve putanje. Međutim, zbog veličine Zemljine senke, koja je oko dva puta veća no što je Mesec, do pomračenja dolazi kada se pun Mesec nađe u kritičnom periodu za pomračenja, odnosno kada je Sunce dovoljno blizu čvorovima Mesečeve putanje. Zbog toga se, osim sarosa koji je prirodni ciklus za pomračenja, mogu izdvojiti i drugi ciklusi pomračenja koji se sa većom ili manjom preciznošcu, u dužem ili kraćem periodu poklapaju, ali se nakon nekog perioda prekinu.

Džerald Hokins dolazi na ideju da je moguće da se bar neki od tih ciklusa može konstatovati dugoročnijim sistematskim praćenjem Meseca. On traži vezu između pomračenja i pozicija na kojima izlazi Mesec, budući da je to praktično jedini parametar koji se dovoljno precizno može uočiti i markirati. U svojim proračunima za period od 2001. do 1000. godine pre nove ere posebnu pažnju je obratio na situacije kada je Mesec izlazio u pravcu stounhendžovog Petnog kamena. Osim toga, određivao je pravce Mesečevog izlaska u vreme oko zimskog solsticijuma. Došao je do zaključka da kada u takvim slucajevima PUN Mesec izlazi u pravcu Petnog kamena, tada dolazi do pomračenja Sunca ili Meseca. Drugim rečima, u takvim slučajevima kritični period za pomračenja pada oko solsticijuma. Na osnovu toga Hokins dolazi do zakljucka da nakon 56 godina, tj. tri obilaska čvorne linije po ekliptici (3 X 18.61 = 55.83, približno 56), pomračenja padaju u isti dan godine (koji se, recimo, mogao meriti od dana solsticijuma) i pretpostavlja da su Obrijeve jameslužile za brojanje godina u jednom 56-ogodišnjem ciklusu. Da bi ova računaljka funkcionisala, bilo je potrebno da se one noći kada se desi pomračenje Meseca, markirni kamen postavi na poziciju koja se nalazi u pravcu Petnog kamena; potom, svake godine, recimo na dan jednog od solsticijuma, marker se pomeri za jednu poziciju udesno. Za 56 godina brojač će ponovo ukazivati na zimsko ‘kratkodnevničko’ pomračenje Meseca. Ako se po istom principu ustanove brojači i za ostala pomračenja sa intervalima od 9, 9, 10, 9, 9, 10 jama, bilo bi moguće predvideti i ostala zimska pomračenja. Osim mogućih nezgoda praktične prirode vezanih za markiranje, postoje i čisto teorijski problemi. Period od 56 godina nije pravi ciklus pomračenja. On je periodičan samo za pomračenja pri takozvanom visokom Mesecu za vreme zimskog solsticijuma, i samo za njih.

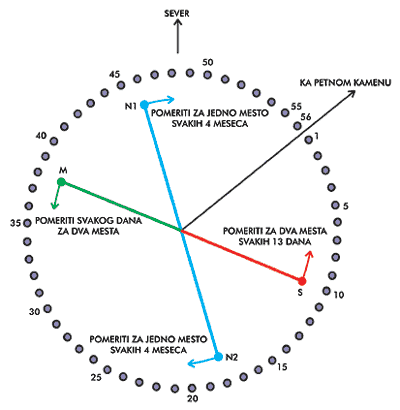
Fred Hojl uzima da Obrijev prsten predstavlja šemu uglovne podele ekliptike. On pretpostavlja da je po rupama bilo moguće premeštati kamenove za markiranje. Prema njemu, Obrijev prsten (može da) funkcioniše i samo kao računaljka za predviđanje pomračenja. Šema programa data je na donjoj slici. Markirni kamen (ili markirno stablo) S prati kretanje Sunca po ekliptici, marker M kretanje Meseca, a N1 i N2 (uvek na suprotnim stranama kruga) prate kretanje čvorova. Kako linija čvorova napravi pun krug po ekliptici za 56 godina, to je dovoljno svake godine pomeriti markere za tri pozicije da bi se nakon tog perioda došlo do iste tačke. Dalje, ako se marker za Mesec pomeri svakoga dana za dve pozicije, nakon 2 x 28 = 56 dana ponovo se dolazi do početne pozicije. Po istom principu, marker S koji prati kretanje Sunca po ekliptici treba pomeriti za dve rupe svakih 13 dana (56 x 13 / 2 = 364 dana, dakle, praktično jedna cela godina). Kada se linija cvorova N1N2 poklopi sa linijom SM, pri cemu se tacke S i M nalaze na suprotnim stranama, desiće se pomračenje Meseca.

Metod je sa astronomskog stanovišta očigledno bolji od onog koji je predložio Hokins. On predviđa sva pomračenja Meseca, dakle i ona koja se sa tog mesta ne mogu videti. Osim Mesečevih predviđa i Sunčeva pomračenja, bez obzira na to što su veoma male šanse da će se ta pomračenja odatle videti. Jedan od ozbiljnih problema je tehničke prirode: kada startovati program (ili ga, možda, restartovati?!). Drugi je problem intelektualno delikatniji, možda pre za nas nego za tadašnje Stounhendžane. U redu je da su imali markere za Sunce i Mesec čije se kretanje očigledno može primetiti, ali kako su došli do toga da uvedu markere i za dve nevidljive tacke, odnosno čvorove? Hojl ima odgovor i za to: možda su ovde radili neki praistorijski Njutn ili Ajnštajn, a Stounhendž je bio svojevrsni univerzitet na kome su se obučavali studenti, tj. buduci ‘astronomi’ za megalitske opservatorije. Manjak pouzdanih činjenica mnoga rešenja čini prihvatljivim. U svakom slučaju, niko ne sumnja u to da tradicija visokog školstva u Britaniji ima duboke korene.

Branislav Savić

Tekstovi o nauci na portalu P.U.L.S.E

  Arheologija, Nauka, Stounhendž