Saga o nuli: Kako je ništa postalo sve – Možda ne deluje logično da su brojevi i numerički sistemi uopšte podložni istoj vrsti konstantne transformacije kao i bilo koji drugi kulturološki fenomeni. Kada se razmatra koncept broja, treba imati u vidu da su uvek bili zavisni od religijskih, društvenih pa čak i prirodnih uslova civilizacije u kojoj su izranjali. Ovo je priča o tome kako je značaj jednog od njih bio uporno zanemarivan, čak i zabranjivan – i kako je, konačno priznat i primenjen, olakšao strelovit rast matematike.

Sama činjenica da je nula uvršćena u zvanični decimalni sistem tek u XIII veku, makar u Evropi, govori u prilog virovitoj prošlosti cifre čija je dvojakost i simboličnost izmicala razumevanju i potrebama pređahnjih kultura. Dualitet o kome je reč čini isprepletanu istoriju nule kao simbola ničega i nule kao broja sa vlastitim matematičkim svojstvima i primenom. Prva, simbolička vrednost nule nosi jednu bitnu karakteristiku broja kao nosioca položaja. Time se misli na značaj njenog fizičkog mesta unutar našeg pozicionog brojnog sistema koji, kao što je slučaj i sa svakom drugom cifrom, određuje vrednost broja (u slučaju broja “2012″, obzirom na naš važeći decimalni sistem sa bazom 10, uloga nule je pivotalna – da nije njenog nedvosmislenog prisustva, taj broj bismo brkali sa 212. Tako i prisustvo dvojke označava broj 2, ali i 2000).

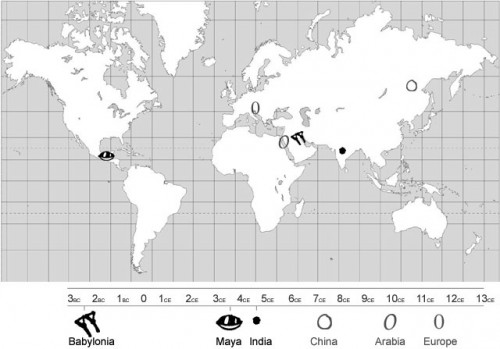
Koliko god to danas delovalo zdravorazumski i podrazumevalo se samo po sebi, nije uvek bilo tako. Povešćemo vas u mali povesni obilazak “brojčanih muzeja” koji su oblikovali istoriju nauke, ekonomije, inženjerstva…. Početna destinacija je Vavilon u III veku p.n.e. gde su se javili prvi zabeleženi tragovi upotrebe nule. Do toga, verovatno, ne bi ni došlo da, najverovatnije usled neke anomalije ili pogreške, kojom je seksagezimalnom sistemu (sa osnovom u broju 60 – ne brkati sa heksadecimalnim sa bazom 16) bio pridružen treći simbol, uz postojeća dva. Sada se, stoga, trebamo upoznati i sa ovim numeričkim sistemom koji se, iako sa osnovom 60, služio samo dvema simbolima za njihovo predočavanje.

Još od 1800. god. p.n.e. na teritoriji Mesopotamije su simboli klina i polumeseca (približno posmatrano, takvi su im bili oblici) različitim tipovima grupisanja formirali brojeve od 1 do 59, čime je na glinenim tablicama računat period prolaska godina. Na primer, broj 124 je formiran uklesavanjem dva klina (dve šezdesetice) i četiri klina (četiri jedinice), kao na slici ispod. Međutim, kako indicirati, npr., broj 3604 – to jest, da nema ničega na određenom mestu u broju? Isprva je iznuđeno rešenje ostavljanja praznog prostora, ali u ređoj meri, jer je od slučaja do slučaja bilo teško ustanoviti da li je prazan prostor uopšte ostavljen. Stoga je neko prilično dovitljiv, verovatno po vokaciji astronom, stvorio simbol koji služi kao separator u vidu duplog iskošenog klina. Bila je to proto-ideja nule, premda još daleko od smisla koji danas nosi.

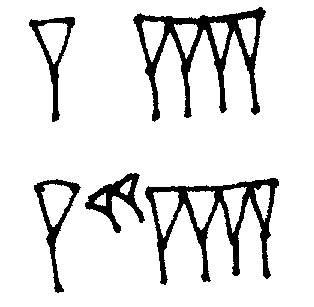
Mnogo hiljada kilometara i vekova kasnije, izolovana i nepoznata ostatku sveta, Majanska civilizacija je neometano prosperirala u otuđenim pejzažima današnje centralne Amerike. Vrsni astronomi, arhitekte i umetnici, ispljavali su enorman nedostatak smisla za praktičnost. Iako je njihov razvoj bio prilično usporen neposedovanjem umeća izrade alata i oruđa, što je čak i bilo seme njihovog pada, imali su veoma kompleksne kalendarske sisteme od kojih je za drugo otkriće nule krucijalan bio tzv. Dugi kalendar, koji je vreme merio od početka njihove civilizacije, 3113. godine p.n.e., do 21.12. tekuće godine.

Majanski brojčani sistem bio je vigezimalni (sa osnovom 20) i vrlo kompleksan u formalnoj upotrebi, sa strogim setom pravila pri grafičkom prikazu. Nula je bila njihov nosilac pozicionog sistema, ali nije bila upotrebljavana u računanju i izložena u vidu oblika školjke.

Šta se u međuvremenu odigravalo u uvek presudnoj Grčkoj? Sasvim sigurno, matematički napredna kultura poput te je morala da se služi svim prednostima pozicionog brojčanog sistema? Pogrešno. Helenska matematika je bila zasnovana na geometriji i brojevi su bili tek način da se simbolički predoči dužina linija. To objašnjava i averziju Grka prema zamisli nule – kakav geometrijski oblik bi korespondirao sa nečim što ne postoji? Kosmologija tog vremena nije bila naklonjena mislima o odsustvu stvari, praznini – koja je bila itekako bezbožnička. Premda postoji jedan značajan momenat – matematičari Jelade koji su beležili astronomske podatke su, veli se, prvi koristili simbol 0 kao notaciju za nulu. Jedna od teorija koja to objašnjava je posredi prvo slovo reči “ouden” sa značenjem “ništa.

Istočno odatle, značaj Indije se pokazao presudnim za razvoj zapadne i opšte prihvaćene matematike kakvu poznajemo danas. Stoga ima nekog romantizma i mistike u faktu da sve današnje prirodno-naučno znanje, ili bar njenu simboličku stranu, dugujemo filozofskim i duhovnim poimanjima cikličnog razvoja na indisjkom potkontinentu. Dok su Grci svoje viđenje kosmogonije i ustrojstva nadredili brojčanom sistemu, odbacujući koncept geometrijskog i svakog drugog ništavila, Indijci takvih muka nisu imali. Štaviše, oni su prvi tretirali brojeve kao čistu apstrakciju, što je ogromna smena do tada vladajuže paradigme po kojoj su brojevi stvarna refleksija fizičke i geometrijske stvarnosti. Bramagupta, astronom i matematičar iz VII veka naše ere, stoji iza ove svojevrsne brojčane reformacije kao njen idejni vođ, iako se smatra da je matematička koncepcija nule prisutna bila prisutna u Indiji desetinama hiljada godina i pre toga.

A iza njegovih novina, kao i uspelih namera očuvanja i prenošenja znanja, stoji jedna interesantna veština pamćenja – takoreći, mali trik. Matematički problemi su se pisali u stihu radi lakše pamtljivosti. Npr., reči stiha “viya dambar akasasa sunya yama rama veda” imaju svoje znaćenje ali i broj – to su “nebo (0) atmosfera (0) prostor (0) praznina (0) primordijalni par (2) Rama (3) Veda (4).

U hinduističkom apstraktnom umu klijalo je još jedno zrno odlučujuće za sudbinu buduće nauke – ideja negativnih brojeva. Zagledavši se u prostor iza nule, najednom se pred ćovekom protezala enormna linija u oba pravca, pozitivnom i negativnom, sa nulom kao polazištem, tj. središnjom tačkom. Upravo je “sunya” iz gore navedenog stiha signaliziralo to ništavilo. To je bilo i konačno nezavisno izumljivanje broja 0 koji je, preko Kambodže, Kine i, konačno, Arapa, dospeo i u Evropu (sama etimologija reči nula (zero) izvedena je iz italijanske “zefiro”, ukorenjene u arapskim “safira” i “sifr” – ništa, koja je sama bila prevod sanskritske reči “sunya” – praznina). U IX veku su udareni konačni temelji dinamičnog brojčanog kanona kojem će se klanjati svi umovi u vekovima koji slede – pozicionog sistema brojeva od 0 do 9. Bilo je to rođenje algebre.

Put je odatle i dalje bio trnovit, ali nezaustavljiv. Od Fibonačijeve knjige “Liber Abaci” iz 1202., nastale na njegovim proputovanjima južnim obalama Mediterana u kojoj sa zanosom piše o “arapskom načinu brojanja”, preko florentinskih trgovaca i bankara, omamljenih upotrebljivošću istočnjačkog principa do zgražavanja florentinskih vlasti koje su se iz petnih žila trudile da ga stave van zakona zbog, kako su tumačili, nebrojenih podložnosti falsifikovanju i prevarama prostim dodavanjem cifre kojom se naduvava vrednost broja.

Cvetanje naučne revolucije umnogome dugujemo teško stečenom ali zasluženom položaju temelja moderne matematike koju nula danas uživa. Dekartovi koordinatni sistemi iz XVII veka, najharmoničniji brak geometrije i aritmetike za koji se i danas zna, bio je konačan trijumf ovog broja prema kojem je čovečanstvo tako neretko bilo ambivalentno. Sada je bio esencijalan; oruđe bez kojeg je i geometrija bila neostvariva, pa čak i asptraktno poimanje kosmičkog porekla – naime, nula je odonda pokretač, primarno stanje infinitezimalnosti iz kojeg je sve poteklo. Od autsajdera do heroja, sitnim koracima koji su se merili epohama.

Za P.U.L.S.E: Andrej Vidović

Um i Spoznaja na portalu P.U.L.S.E

  Andrej Vidović, istorijat, Matematika, Nauka, nula