U potrazi za tehnologijom po meri čoveka
In memoriam Dr. Lotfi A. Zadeh 1921-2017

Termin fazi potiče od prof. Lotfija Zadeha (1921-2017) sa Univerziteta u Berkliju, stručnjaka za oblast upravljanja, koji je 1965. u radu “Fazi skupovi” za časopis “Informacione nauke” napisao:
Da bi se izborili sa veoma složenim problemima, ne moramo da se krećemo ka rigoroznosti, što većoj preciznosti opisa i razmišljanja o pojavama, već možemo da krenemo i u suprotnom smeru i dozvolimo da opisi budu neprecizni u duhu prirodnog jezika.
Povećanjem nepreciznosti iskaza, ponekad postajemo razumljiviji za sagovornika. Na primer, iskaz „Devojka je lepa“ za većinu ljudi je razumljiviji od iskaza „Lepotu devojke na skali od 1 do 10 ocenjujem sa 8,7“. Fazi pristup, pored nepreciznosti, karakteriše i mekoća, postepenost prelaza od jedne do druge krajnosti, npr. od ukusnog do neukusnog jela. U fazi logici, iskaz je istinit u izvesnom stepenu. Fazi logika omogućava da subjektivne iskaze obrađujemo pomoću računara i zato se tehnologije koje koriste fazi pristup (fazi tehnologije), smatraju humanim.
Pre nego što su primenjene na obradu prirodnog jezika pomoću računara (Natural Language Processing), fazi tehnologije su svoje mesto našle u automatici. U Japanu je primena fazi tehnologije unapredila ekonomičnost, udobnost i preciznost vozova i metroa. Fazi logika je uspešno primenjena i na prepoznavanje rukopisa, predviđanje zemljotresa i modeliranje emocija.
Istina u izvesnoj meri
Fazi logika odbacuje aksiome klasične logike. U fazi logici važi: i P i ne-P mogu da važe istovremeno u izvesnom stepenu. Aristotelova logika nam pomaže da iz “Svaki Grk je čovek” i “Svaki čovek je smrtan” izvedemo zaključak “Svaki Grk je smrtan” ali nam je neophodna fazi logika da bismo iz “Ako je jabuka crvena, onda je zrela” izveli zaključak “Ako je jabuka skoro crvena, onda je skoro zrela”.

Fazi skup predstavlja skup elemenata sa sličnim (a ne neophodno istim) svojstvima. Stepen pripadnosti fazi skupu nekog elementa iz domena skupa može da ima vrednost u opsegu od 0 do 1, pri čemu 0 i 1 označavaju granične slučajeve, pri kojima element uopšte ne pripada ili u potpunosti pripada skupu, kao kod klasičnih, diskretnih skupova. Zapravo, fazi skupovi su proširenje i uopštenje diskretnih skupova tako da granice skupova ne moraju da budu oštre. Mekoća granica fazi skupova je analogna mekoći granica univerzalija u prirodnom jeziku. Matematička funkcija definisana nad domenom fazi skupa koja određuje stepen pripadnosti elemenata tom skupu zove se fazi funkcija pripadnosti i najčešće obeležava sa m(x).
Fazi matematika: x=prohladno
Lingvistička (fazi) promenljiva je ona čije su dozvoljene vrednosti reči prirodnog jezika. Na primer lingvistička promenljiva temperatura može imati vrednost veoma hladno, hladno, prohladno, sveže, prijatno, toplo, veoma toplo, vruće i vrelo. Reči veoma, pomalo, baš, manje-više, pomalo, nazivaju se lingvističkim modifikatorima (hedges) koji se primenjuju na osnovne lingvističke vrednosti, na primer toplo i hladno. U opštem slučaju, vrednosti lingvističkih promenljivih se dobijaju kombinovanjem modifikatora, veznika i osnovnih vrednosti, na primer: pomalo hladno, veoma toplo, ni toplo ni hladno. Vrednosti lingvističkih promenljivih u fazi terminologiji odgovaraju univerzalijama u metafizičkoj terminologiji.
Lingvističke promenljive mogu opisivati merljive (npr. temperatura, visina, uzrast) ili direktno nemerljive (npr. lepota, dobrota, duhovnost) osobine. Promenljiva koja opisuje istu osobinu kao i merljiva lingvistička promenljiva, ali egzaktno, obično numerički, naziva se osnovnom promenljivom. Na primer, dob ljudskog života se može označiti lingvističkom promenljivom čije su moguće lingvističke vrednosti elementi skupa {mlad, sredovečan, star, veoma star, baš mlad…} ili osnovnom promenljivom „starost osobe u godinama“ koja može da ima neku od vrednosti iz proširenog skupa prirodnnih brojeva, N0. Relacija između vrednosti osnovne promenljive i vrednosti lingvističkih promenljivih može da se modelira pomoću funkcije pripadnosti osnovne promenljive fazi skupu vrednosti lingvističke promenljive. Na sledećem grafikonu prikazane su moguće funkcije pripadnosti starosti osobe u godinama, fazi skupovima određenim vrednostima lingvističke promenljive doba života. „Mlad“ i „star“ nesumnjivo spadaju u osnovne lingvističke vrednosti, dok se „sredovečan“ može tumačiti kao osnovna lingvistička vrednost ali i kao modifikovana vrednost osnovnih lingvističkih vrednostih – ni mlad, ni star. Funkcija pripadnosti skupu sredovečnih ljudi na grafikonu, modelirana je trapezoidnim oblikom, koji se često upotrebljava za modeliranje funkcija pripadnosti. Oblici „levo rame“ i „desno rame“ (left-shoulder, right-shoulder), koji su ovde upotrebljeni za modeliranje stepena pripadnosti fazi skupovima mladih, odnosno starih ljudi respektivno, posebni su slučajevi trapezoidnog oblika funkcije pripadnosti.
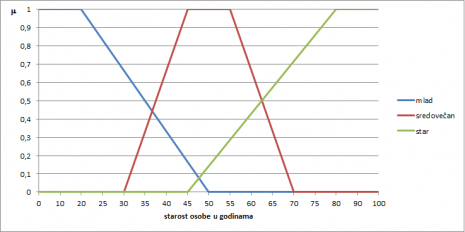
Sa grafikona je vidljivo da u ovakvom modelu osoba koja ima 35 godina pripada fazi skupovima mladih i sredovečnih ljudi sa stepenom pripadnosti mml(35)=0,5 odnosno msr(35)=0,33. Ta osoba ne pripada fazi skupu starih ljudi zato što je mst(35)=0. Osoba koja ima 47 godina u potpunosti pripada fazi skupu sredovečnih ljudi msr(47)=1, ali takođe pripada skupovima mladih i starih ljudi sa malim stepenom pripadnosti. Proces u kome na osnovu funkcija pripadnosti fazi skupovima dolazimo do jednoznačnog zaključka, odluke ili kvalifikacije zove se defazifikacija. Na primer, na osnovu funkcija pripadnosti iz prethodnog primera i metoda izbora onog fazi skupa za koju funkcija pripadnosti ima najveću vrednost, defazifikacijom izvodimo zaključak da je osoba stara 55 godina sredovečna.
Funkcije pripadnosti vrednostima lingvističkih promenljivih obično definišemo intuitivno, na osnovu prethodnog znanja o svetu. Proces kreiranja funkcije pripadnosti zove se fazifikacija.
Koliko ste mladi?
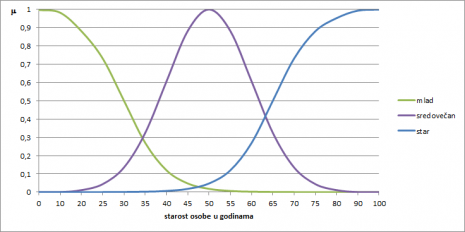
Iako se često koriste zbog jednostavnosti, trapezoidne funkcije pripadnosti nisu idealan model funkcija pripadnosti fazi skupu vrednosti lingvističke promenljive. Prelomi u uglovima trapezoida nisu model nekog postojećeg fenomena u modeliranom domenu. Pored toga, zbog različitog konteksta upotrebe lingvističkih promenljivih, u realnosti gotovo da ne postoji opseg egzaktne ulazne promenljive x za koju je vrednost funkcije pripadnosti m(x)=0 ili m(x)=1. Na primer, u kontekstu razgovora korisnika usluga staračkog doma, nije neobično da se 75-godišnjak okarakteriše kao mlad. S druge strane, dete uzrasta 12 godina je već previše staro za polazak u redovnu osnovnu školu. Zbog toga je za funkcije pripadnosti skupovima vrednosti lingvističke promenljive koje predstavljaju krajnosti opsega (mlad, star) bolji izbor sigmoidna, a za vrednosti koje predstavljaju sredinu opsega (sredovečan) gausovska funkcija pripadnosti. Te funkcije su prikazane na sledećem grafikonu.
Magični broj 7
Iz ovako modelirane lingvističke promenljive „doba života“, jasnije se vidi da postoje životna doba (npr. 35 godina, 63 godine) u kojima se starost osobe ne može ni sa relativnom sigurnošću iskazati nijednom od osnovnih lingvističkih vrednosti, tj. vrednost funkcije pripadnosti je manja od 0,5 za sve tri lingvističke vrednosti – mlad, sredovečan i star. Očigledno je da kardinalnost skupa lingvističkih vrednosti mora da bude veća od tri da bi preciznije izražavanje bilo moguće. U lingvističkom modeliranju, obično se koriste skupovi kardinalnosti sedam ili devet. Te vrednosti odgovaraju rezultatima istraživanja jednog od utemeljivača kognitivne psihologije, Henrija Milera, koji pokazuju da je granica broja kategorija u koje prosečan čovek može sa relativnom sigurnošću da razvrsta perceptivni doživljaj – sedam. U domenima u kojima nema adekvatnih osnovnih lingvističkih vrednosti, dodatna granulacija se postiže upotrebom modifikatora – više-manje mlad, veoma star…
Istraživači koji su se bavili fazi skupovima, na prvom mestu Zadeh, razvili su matematičke metode pomoću kojih može da se odredi funkcija pripadnosti fazi skupu modifikovane lingvističke vrednosti ukoliko je poznata funkcija pripadnosti fazi skupa osnovne lingvističke vrednosti. Tako se za modifikator „veoma“ uobičajeno koristi kvadrat vrednosti osnovne funkcije, a za modifikator „manje-više“ kvadratni koren funkcije pripadnosti osnovne funkcije. Na primer, na sledećem grafikonu je pored fazi funkcije pripadnosti skupu starih osoba, prikazana i fazi funkcija pripadnosti skupu veoma starih osoba, izvedena po formuli mvst(x)=(mst(x))2
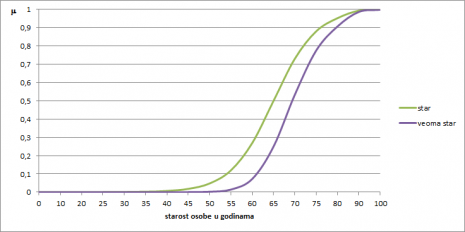
Sa grafikona se vidi da, sa izabranim parametrima sigmoidne funkcije, osoba koja ima 65 godina pripada fazi skupu starih osoba sa stepenom pripadnosti 0,5 ali je stepen pripadnosti te osobe skupu veoma starih osoba tek 0,52= 0,25.
Fazi logika i verovatnoća
Treba reći da u naučnoj zajednici, uprkos uspešnim primenama, ne postoji jedinstvo u pogledu posebnosti i značaja fazi logike. Fazi logika i verovatnoća su dva načina izražavanja neizvesnosti. Razlika je u tome što fazi logika razmatra koliko je element u skupu, a verovatnoća koliko je verovatno da je element u skupu, podrazumevajući i dalje samo dve moguće vrednosti funkcije pripadnosti – pripada ili ne pripada. Iako je filozofska razlika očigledna, još uvek su otvorene rasprave o tome da li fazi logika kao alat donosi praktičnu korist u odnosu na klasičnu verovatnoću i da li je matematički svodiva na klasičnu logiku.
Za P.U.L.S.E: Nikola Petrović Morena
Tekstovi o nauci na portalu P.U.L.S.E
Stavovi autora ne odražavaju nužno uređivačku politiku P.U.L.S.A. Impresum.
Podrži P.U.L.S.E
P.U.L.S.E je prostor za mišljenje, sumnju i odgovornost. Ako ti je taj prostor važan, omogući nam da ostane otvoren.
Podrži na PatreonuIli putem PayPala:

You must be logged in to post a comment Login