Hilbertov hotel – Krajem februara sam dobio e-mail poruku od čitaoca pod imenom Kim Forbs. Njen šestogodišnji sin Ben pitao ju je matematičko pitanje na koje ona nije mogla odgovoriti, a ona se nadala da bih ja mogao da pomognem:
Danas je 100. dan u školi. Bio je veoma uzbuđen i rekao mi je sve što zna o broju 100, uključujući i to da je 100 paran broj. Tada mi je rekao da je 101 neparan broj i 1 milion je paran broj, itd. On se tada zaustavio i upitao: ”Da li je beskonačnost parna ili neparna”.
Objasnio sam mu da beskonačnost nije ni parna ni neparna. Nije broj u uobičajenom smislu, i ne poštuje pravila aritmetike. Sve vrste protivurečnosti bi ga pratile da jeste. Na primer, “ako bi beskonačnost bila neparna, onda je 2 puta beskonačnost parno. Ali oba su beskonačna! Dakle, cela ideja o parnosti i neparnosti nema smisla za beskonačnost.
Kim je odgovorila:
Hvala. Ben je bio zadovoljan sa tim odgovorom. Dopada mu se ideja da je beskonačnost dovoljno velika da bude i parna i neparna.
Iako se nešto iskvarilo u prevodu (beskonačnost nije ni parna ni neparna, a ne oba), Benovo rezonovanje nagoveštava veću istinu. Beskonačno može biti umno izazovna. Neke od njenih najčudnijih aspekata prvi put su došle na svetlo kasnih 1800-ih, sa pionirskim radom Georga Kantora (Georg Cantor) na “teoriji skupova”. Kantor je bio posebno zainteresovan za beskonačne skupove brojeva i tačaka, poput skupa {1, 2, 3, 4, … } “prirodnih brojeva” i skupa tačaka na liniji. On je definisao strog način da uporedi različite beskonačne skupove i otkrio je, šokantno, da su neke beskonačnosti veće od drugih.
U to vreme, Kantorova teorija je izazvala ne samo otpor, već i bes. Anri Poenkare (Henri Poincaré), jedan od vodećih matematičara tog doba, nazvao je to bolešću, ali drugi gigant ere, Dejvid Hilbert (David Hilbert), video je to kao trajan doprinos i kasnije je proglasio:“Niko nas ne sme proterati iz Raja koji je Kantor stvorio.”
Moj cilj ovde je da vam odškrinem ovaj raj. Ali, umesto da radimo direktno sa skupom brojeva ili tačaka, dozvolite mi pristup koji je uveo sam Hilbert. On je živahno preneo čudnost i neobičnost Kantorove teorije pričajući alegoriju o velikom hotelu, sada poznatom kao Hilbertov hotel. Uvek je solidno popunjen, ali uvek postoji prazno mesto. Hilbertov hotel ne samo da ima na stotine soba – ima beskonačan broj njih. Kad god stigne novi gost, menadžer prebaci stanara sobe 1 do sobe 2, sobu 2 do sobe 3, i tako dalje. To oslobađa sobu 1 za novajliju, a i dalje su smešteni i svi ostali (uprkos neprijatnosti zbog premeštanja).
Sada pretpostavimo da beskonačno mnogo novih gostiju pristigne,znojavi i naprasiti. Nema problema. Uvek spokojan menadžer prebaci stanara sobe 1 do sobe 2, iz sobe 2 do sobe 4, sobe 3 u sobu 6, i tako dalje. Ovaj trik dupliranja otvara sve neparne sobe – beskonačno mnogo njih – za nove goste. Kasnije te noći, beskrajni konvoj autobusa protutnji do recepcije. Postoji beskonačno mnogo autobusa, i što je još gore, svaki je pun beskonačno mnogo tvrdoglavih ljudi koji zahtevaju da hotel dokaže svoj moto:
Uvek imate slobodnu sobu u Hilbertovom hotelu.
Menadžer se suočio sa ovim izazovom i ranije i olako ga preuzima. Prvo on radi trik dupliranjem. Prebacuje trenutne goste u parno numerisane sobe i oslobađa sve neparne – dobar početak, jer sada ima beskonačan broj soba na raspolaganju. Ali da li je to dovoljno? Da li ima zaista dovoljno neparnih soba za smeštaj obične horde novih gostiju? Izgleda malo verovatno, jer tamo je nešto kao “beskonačnost na kvadrat” ljudi koji zahtevaju te sobe. (Zašto kvadrirana beskonačnost? Zato što se radilo o beskonačnom broju ljudi u svakom od beskonačnog broja autobusa i to iznosi beskonačnost puta beskonačnost, šta god to značilo.) Ovo je mesto gde logika beskonačnosti postaje veoma uvrnuta.
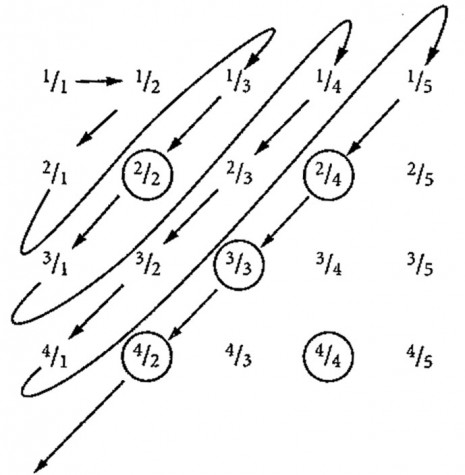
Da bi se razumelo kako će menadžer rešiti svoj najnoviji problem, pomaže vizuelizacija ljudi koje mora da usluži:
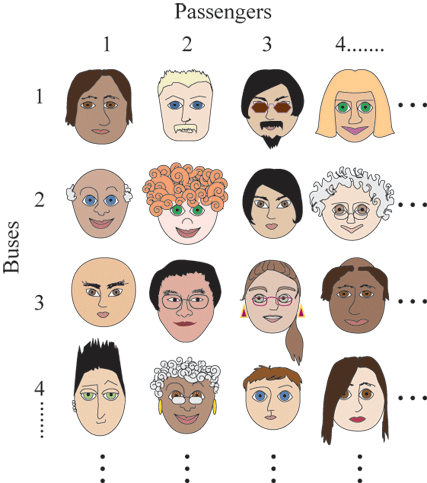Naravno, ne možemo prikazati bukvalno sve od njih, jer dijagram bi morao da bude beskonačan u oba smera. Ali, konačna verzija slike je adekvatna. Poenta je da je za bilo kog određenog putnika autobusa (vaša tetka Inez, recimo, na odmoru iz Luizvila) sigurno da će se pojaviti negde na dijagramu, samo ako uključimo dovoljno redova i kolona. U tom smislu, uračunat je svako iz svakog autobusa. Izaberete putnika, a on ili ona će se sigurno pojaviti u nekom konačnom broju koraka istočno i južno od ugla dijagrama.
Menadžerski izazov je naći način za rad kroz ovu sliku sistematično. On treba da osmisli plan za dodeljivanje sobe tako da svako dobije na kraju jednu, posle samo konačnog broja drugih ljudi koji su usluženi.
Nažalost, prethodni menadžer nije razumeo ovo i desio se haos. Kada se sličan konvoj pojavio na njegovom satu, on je usplahiren pokušavao da obradi sve ljude iz autobusa 1 tako da nikada nije uspeo da stigne do bilo kog drugog autobusa, ostavljajući sve one zapostavljene putnike da viču i besne. Vizuelno na dijagramu dole, ova kratkovida strategija bi odgovarala putanji marševske kolone ka istoku duž reda 1, nikada se ne vraćajući nazad.
Novi menadžer, međutim, ima sve pod kontrolom. Umesto da teži samo jednom autobusu, on ide cik – cak kroz dijagram, krećući iz ugla kao na slici ispod.
On počinje sa putnikom 1 iz autobusa 1 i daje joj prvu praznu sobu. Druga i treća prazna soba idu putniku 2 iz autobusa 1, zatim putniku 1 iz autobusa 2, od kojih su oba prikazana na drugoj dijagonali od ugla dijagrama. Po usluživanju njih, menadžer prelazi na treću dijagonalu i predaje u ruke skup ključeva sobe putniku 1 iz autobusa 3, putniku 2 iz autobusa 2, i putniku 3 iz autobusa 1.
Nadam se da je menadžerov postupak – prelaska sa jedne dijagonale na drugu – jasan sa slike gore i da ste uvereni da će se do neke određene osobe stići u konačnom broju koraka.
Dakle, kao što je reklamirano, uvek ima soba u Hilbertovom hotelu.
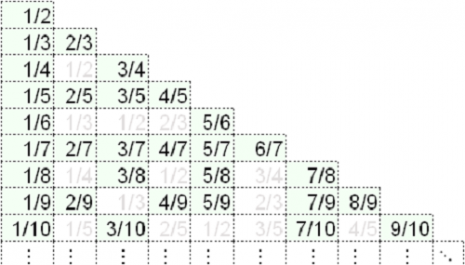
Argument koji sam Vam upravo predstavio je poznat u teoriji beskonačnih skupova. Kantor ga je koristio da dokaže da ima tačno toliko pozitivnih razlomaka (odnos p/k pozitivnih celih brojeva p i k), koliko ima prirodnih brojeva (1, 2, 3, 4,…). To je mnogo jača tvrdnja nego reći da su oba skupa beskonačna. Kaže se da su beskonačni u tačno istoj meri, u smislu da je “jedan-na-jedan (1-1) preslikavanje” moguće uspostaviti između njih.
Možete gledati na ovo preslikavanje kao na prijateljski sistem u kome je svaki prirodan broj uparen sa nekim pozitivnim razlomkom i obrnuto. Postojanje ovakvog prijateljskog sistema izgleda potpuno u suprotnosti sa zdravim razumom – to je vrsta sofistike koja je naterala Poenkarea na užasavanje. Za to se podrazumeva da smo mogli napraviti detaljnu listu svih pozitivnih razlomaka, čak iako ne postoji najmanji! A ipak postoji takav spisak. Već smo ga našli. Razlomak p/k odgovara putniku p iz autobusa k, a argument gore pokazuje da je svaki od ovih razlomaka moguće upariti sa nekim prirodnim brojem 1, 2, 3,… datim brojem sobe putnika u Hilbertovom hotelu.
Coup de Grace (udar milosrđa) je Kantorov dokaz da su neki beskonačni skupovi veći od ovog. Konkretno, skup realnih brojeva između 0 i 1 je “neprebrojiv” – ne može se staviti u “1-1” preslikavanje sa prirodnim brojevima. Za ugostiteljstvo to znači da ako se svi ovi realni brojevi prikazuju na recepciji i pritiskaju zvonce, neće biti dovoljno soba za sve njih, čak i u Hilbertovom hotelu. Dokaz je dat kontradikcijom. Pretpostavimo da se svakom realnom broju može dati sopstvena soba. Tada spisak putnika, na osnovu njihovih decimalnih razvoja i liste soba treba da izgleda ovako:
Soba 1: .6708112345 …
Soba 2: .1918676053 …
Soba 3: .4372854675 …
Soba 4: .2845635480 …
Zapamtite, ovo bi trebalo da bude kompletna lista. Svaki realan broj između 0 i 1 bi trebalo da se pojavi negde, na nekom konačnom mestu na spisku. Kantor je pokazao da dosta brojeva nedostaje iz bilo koje ovakve liste; to je kontradiktorno. Na primer, da se nađe onaj koji se ne pojavljuje nigde na spisku prikazanom gore, idite niz dijagonalu i izgradite broj iz boldovanih cifara:
Soba 1: .6708112345 …
Soba 2: .1918676053 …
Soba 3: .4372854675 …
Soba 4: .2845635480 …
Decimalni broj tako dobijen je .6975 …
Ali još uvek nismo završili. Sledeći korak je uzeti taj decimalni broj i promeniti sve njegove cifre, zamenjujući svaku od njih sa bilo kojom cifrom između 1 i 8. Na primer, mogli bismo da promenimo 6 na 3, 9 na 2, 7 na 5, i tako dalje. Ovaj novi decimalni broj .325 … je ubica. Taj sigurno nije u sobi 1, jer je drugačiji od prve cifre broja tamo. Takođe, nije ni u sobi 2, jer se druga cifra ne slaže. U principu, ona se razlikuje od n-tog broja u n-tom decimalnom mestu. Sledi da se taj broj ne pojavljuje nigde na spisku!
Zaključak je da Hilbertov hotel ne može da ugosti sve realne brojeve. Jednostavno postoji previše njih, beskonačnost iza beskonačnosti.
Steven Strogatz
Tekstovi o nauci na portalu P.U.L.S.E
Hilbertov hotel napisao/la P.U.L.S.E dana
Pregled tekstova autora – P.U.L.S.E →