Borhes – “Vrt sa stazama koje se račvaju”
Borhesova priča “Vrt sa stazama koje se račvaju” može poslužiti jednom neuobičajenom postupku a to je geometrijskoj analizi konstrukcije priče. Geometrija, kao osnova svega postojećeg i kao narativna strategija u ovoj Borhesovoj priči je primenjena na likove, na samu priču kao i na njene različite podnivoe.
“Vrt sa stazama koje se račvaju” ispoveda u svojim poslednjim časovima života Ju Cun, profesor engleskog jezika i nemački špijun u Velikom svetskom ratu. Bežeći od Irca Madena koji radi u službi Engleske, Ju Cun smišlja jedini mogući plan (kako sam Borhes u prologu “Maštarija” kaže, tek poslednji pasus u priči otkriva šta se i zašto u priči dešava) kako da prenese nemačkom vođi ime tajne engleske lokacije koju treba napasti. Posećuje Stivena Alberta, uglednog sinologa. Njih dvojica diskutuju o lavirintu-knjizi (stalnoj Borhesovoj opsesiji) sa imenom “Vrt sa stazama koje se račvaju, delu Cui Pena, Ju Cunovog pretka.
Cui Pen, guverner provincije Junan, astronom, astrolog, šahista, pesnik i kaligraf, koga je na kraju ubio stranac, posvetio je trinaest godina izgradnji haotičnog romana i lavirinta “u kome će se svaki čovek izgubiti’. Albert rešava misteriju koja okružuje oba dela, objašnjavajući da su ’knjiga i lavirint jedno te isto’. Umesto fizičkog lavirinta koji se grana u prostoru, Cui Pen je konstruisao izmišljen lavirint koji se račva u vremenu.
Ubivši Alberta, Ju Cun ispunjava svoju misiju, jer hapšenjem i objavljivanjem vesti u novinama, on zapravo obelodanjuje ime grada sa imenom Albert svom nemačkom zapovedniku. Sam Borhes nas ipak, podatkom iz Istorije evropskog rata Lidela Harta, u uvodnom paragrafu obaveštava da je Ju Cunova misija prouzrokovala samo manje kašnjenje britanskog napada. Borhes, pisac same priče, simetričan je Cui Penu, piscu Vrta – drugom nivou priče. Odgonetanjem lavirinta i umiranjem od ruke stranca, uspostavljena je simetrija između Alberta i Cui Pena. Ju Cun je povezan sa Madenom, a obojica u službi zemalja koje nisu njihove. Oni su takođe simetrični sa strancem X koji je ubio Cui Pena sa svojstvom progonitelja i ubice. Refleksijom kao metaforom, ubice postaju žrtve i obrnuto, kroz pojam beskonačnog račvanja. Da bi se stvorio geometrijski obrazac koji formira beskonačnost potrebno je definisati osnovnu jedinicu fikcije i proučiti načine na koje se ona širi na ostale jedinice i priče.
Borhesov “Vrt….” je predstavljen kružnicom sa Borhesom u centru.

Ju Cunova priča generiše drugi centar kružnice koja je smeštena na prvoj kružnici (budući da je Ju Cun bit Borhesove fikcije). Dva oblika se presecaju u dvema tačkama koje zauzimaju Albert i Maden.
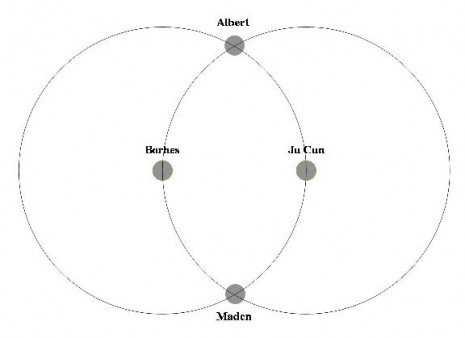
Treća priča je Albertova interpretacija Cui Penove knjige. Još jedan krug je formiran sa Albertom u centru presecajući prethodna dva kruga u tačkama u koje se smeštaju Cui Pen i nepoznati ubica i rezultujući novim krugom.
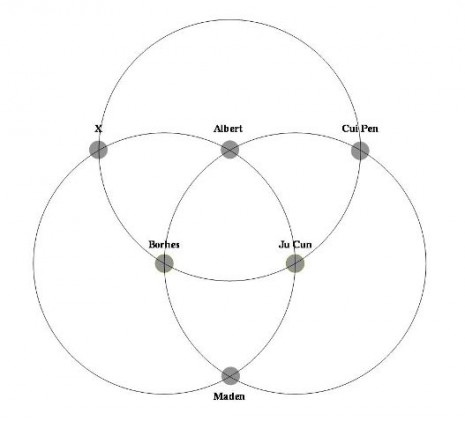
Maden, hapseći Ju Cuna obelodanjuje priču novinama što vodi do sledećeg kruga. Nemački vođa, koji leži u centru narednog kruga konačno odgoneta ovu priču.
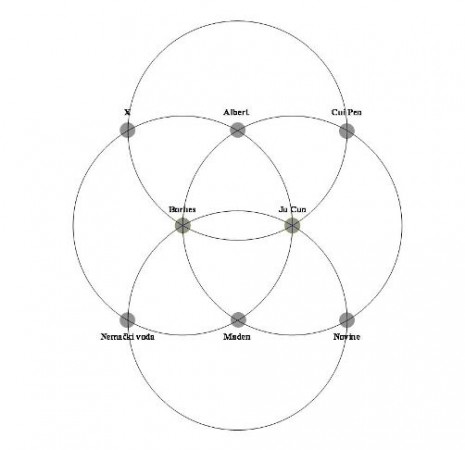
Ovaj obrazac, može da raste beskonačno formirajući mrežu trouglova I čvorova koji se prostiru u svim pravcima izražavajući obrazac račvajućih staza. Svi čvorovi su međusobno simetrični bazirani na translaciji. Krugovi su konstruisani pomeranjem njihovih centara duž tri ose. U ovoj priči obrazac je trougaono popločavanje ravni kao metafora pokrivanja svih mogućnosti.
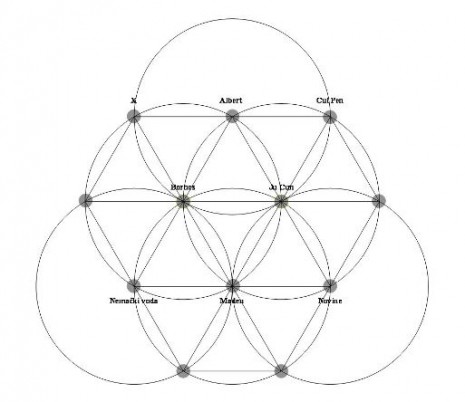
“…Zastao sam, prirodno, kod rečenice: ostavljam različitim budućnostima (ne svim) svoj vrt sa stazama koje se račvaju. Razumeo sam gotovo istog trena; vrt sa stazama koje se račvaju zapravo je nesređeni roman; izraz raznim budućnostima (ne svim) nagovestio mi je sliku račvanja u vremenu, a ne u prostoru…”
Ponovno čitanje celog dela potvrdilo je ovu teoriju. U svim izmaštanim tekstovima, kad god se neki lik suoči sa više mogućnosti, po pravilu se opredeljuje za jednu i odbacuje druge; u svom gotovo nerazmrsivom tekstu, Cui Pen se opredeljuje – i to u isti mah – za sve mogućnosti. Na taj način on stvara različite budućnosti i različita vremena, koji se takođe umnožavaju i račvaju.

Pravilan i proširen, obrazac presecanih krugova je konstruisan da zahvata geometrijsku strukturu pripovesti i pojma beskonačnog prostranstva priča.
za P.U.L.S.E: Boban Savković
literatura: “Matematika u književnosti” Jelena Ćulafić



odličan ti lavirint, a i fizionomiju si mu pogodio.
Simetrije su dobro odredjene, ali “Matematici u književnosti” nedostaju osnovi teorije književnosti – sve je podredila svojoj disciplini.
Na primer: Borhesov krug mora biti takav da obuhvata sve ostale krugove i da ih “nadzire” jer prva ličnost koju pisac stvori je – ko piše tekst, sa koje tačke gledišta sve posmatra. Onda književni likovi ne mogu biti identični ni po kom osnovu pa ne mogu imati krugove istog prečnika…. Različite budućnosti i različita vremena takodje…
Kad se još uključe različite recepcije čitalaca, onda od Matematike u književnosti ostaje samo matematika.
Zašto bi morao biti (Borhesov krug, pogotovo kad je on u pitanju) veći od ostalih? Upravo je Borhes bio pisac takvog profila da nije mario za osnove teorije književnosti. Često su likovi (izmišljeni ili ne) u njegovim pričima nadilazili njega kao “primarnog pisca”. Ali, ako to ostavimo po strani, namera ovog rada bila je, da se putem geometrije, dodatno dokumentuje osnovna intencija priče, romana-lavirinta koji se beskrajno račva u prostoru i vremenu. I ovi krugovi i osnovne tačke u kojima se presecaju tvore to beskonačno prostiranje priče. Borhes, kao pisac, tu nema potrebe biti primarni krug koji obuhvata sve ostale jer bi to bilo u suprotnosti sa osnovnom idejom priče.
Mario / ne mario za teoriju književnosti oni je tu, kao sinteza zanata koji stvara opsenu da “Često su likovi (izmišljeni ili ne) u njegovim pričima nadilazili njega kao “primarnog pisca”. ”
Zatim:
“U ovoj priči obrazac je trougaono popločavanje RAVNI kao metafora pokrivanja svih mogućnosti.”
“… izraz raznim budućnostima (ne svim) nagovestio mi je sliku račvanja u vremenu, a ne u prostoru…”
– a to podrazumeva četiri dimenzije (i vreme/prostor) a ne dve
Namera je lepa, ali je treba izvesti nekom drugom matematikom. Medjutim, tada se ne bi dobio kristal nego kontrolisani haos.
Mario ne mario za teoriju književnosti (a nije toliko jel’te?)…Borhes je učinio (ne samo za književnost) više od mnogih koji za nju bezuslovno mare.
“..izraz raznim budućnostima (ne svim) nagovestio mi je sliku račvanja u vremenu a ne u prostoru…”
Naglasak je na vremenu a ne na prostoru (koji je najmanje trodimenzionalan) a dimenzije vremena su nepoznanica. Zarad pojednostavljena upotrebljeno je trougaono popločavanje RAVNI kao metafora pokrivanja svih mogućnosti, a mislim da bi efektnije ta metafora mogla biti izražena prostornom – trodimenzionalnom – geometrijom, upotrebom nacrtne geometrije kao metode, za šta, nadam se da ćete razumeti, nije bilo dovoljno vremena a i dizajn sajta to ne dozvoljava. Ni to, čini mi se , ne bi Vas razuverilo u Vašoj skepsi, što je Vaše potpuno pravo.
I da…ne postoji “neka druga” matematika. Samo podvrste jedne jedine – i moguće – matematike